[Data Science] Dog Classification

Dog Classification

 

이 문제는 Accuracy를 아는지 묻는 문제였다. Accuracy는 내가 푼 문제 중에 몇 개나 맞췄는지에 대한 지표로, 이 문제에서는 Accuracy가 가장 높게 나오는 최적의 threshold를 찾아야 한다.

 

 

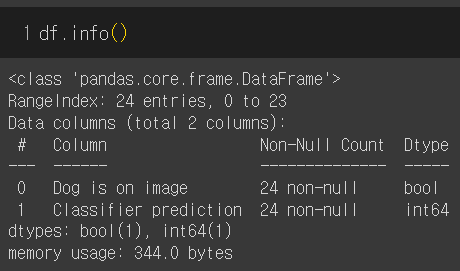
일단, 데이터를 복사해서 메모장에 csv 파일로 저장하고 불러왔다. 샘플 수는 24개고 컬럼은 2개다. "Dog is on image" 컬럼이 target(label)이고, "Classifier prediction" 컬럼이 분류기를 통해 나온 예측값이다. Binary classification 문제이므로 threshold를 정해 예측값(보통 확률값)이 threshold 이상이면 True(1), 미만이면 False(0)로 정한다.

 

 

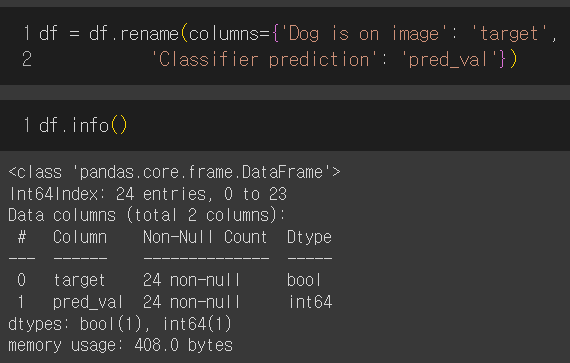
문제에서 주어진 컬럼명은 길고 명료하지 않으므로 target과 pred_val로 바꾼다.

 

 

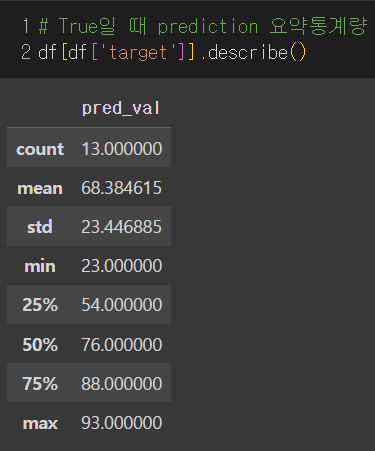
target이 True일 때(즉, Dog일 때) pred_val은 평균 68, 최소 23, 최대 93이다.

 

 

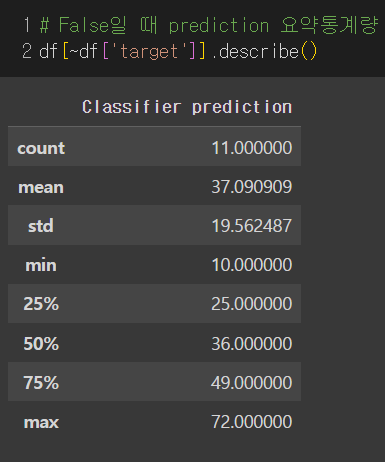
target이 False일 때(즉, Dog가 아닐 때) pred_val은 평균 37, 최소 10, 최대 72이다.

 

 

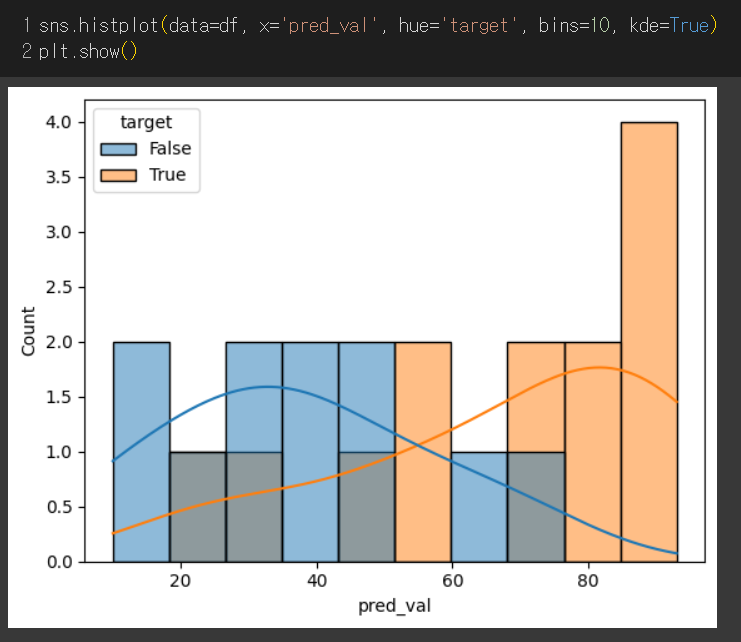
dog일 때와 dog가 아닐 때 두 분포가 서로 구분되는 지점을 찾아야 한다. 이 두 커널 밀도 함수의 접점이 최적의 threshold라 생각하고 커널 밀도 함수를 구하려 했는데 내가 KDE에 대해 잘 모르고 있다는 사실을 깨달았다. 

 

Kernel Density Estimation (커널 밀도 추정) · Seongkyun Han's blog

 

위 블로그가 설명이 잘 되어 있어 자세한 설명은 생략하고, 간단히 말하자면 KDE(Kernel Density Estimation)는 확률 밀도 함수(probability density function, pdf)를 커널 함수를 통해 추정(estimation)한 것이다. 말 그대로 관측된 데이터만으로 "추정"한 거라 막대의 개수(혹은 구간)에 따라 히스토그램이 다르게 그려지듯이 커널 밀도 함수도 bandwidth 파라미터에 의해 첨도가 달라진다. 그 말은 즉슨, 실제 그래프도 아닌 추정한 그래프의 접점으로 최적의 threshold를 찾기는 어렵다. 심지어, bandwidth 파라미터에 의해 그래프가 다르게 그려질 수 있으니 더더욱 이 함수로 구할 수 없다.

완전 탐색

max_cnt = 0
opt_thr = 0
for thr in range(0, 101, 1):
    df['pred'] = np.where(df['pred_val'] >= thr, True, False)
    correct_cnt = df[df['target'] == df['pred']].shape[0]
    if correct_cnt > max_cnt:
        max_cnt = correct_cnt
        opt_thr = thr

print(opt_thr)

 

그래서 threshold를 0 ~ 100 사이를 모두 탐색하면서 맞춘 개수가 가장 많은 threshold를 찾도록 했다. 그런데 이 방법 말고 더 빠른 방법이 없을까? 꼭 모든 threshold를 탐색해야 할까?

선택 탐색

max_cnt = 0
opt_thr = 0

high = int(df[df['target']]['pred_val'].mean())
low = int(df[~df['target']]['pred_val'].mean())

for thr in range(low, high + 1, 1):
    df['pred'] = np.where(df['pred_val'] >= thr, True, False)
    correct_cnt = df[df['target'] == df['pred']].shape[0]
    if correct_cnt > max_cnt:
        max_cnt = correct_cnt
        opt_thr = thr

print(opt_thr)

 

구글링 하다가 dog일 때 평균값과 dog가 아닐 때의 평균값 사이만 탐색하는 풀이를 발견했다. 왜 이 생각을 못했을까? 평균값이나 중앙값 같이 분포의 중심을 나타내는 대푯값을 이용해 두 분포가 어디에서 구분되는지 탐색의 범위를 줄일 수 있다.

 

https://github.com/zcemycl/algoTest/blob/main/py/tests/testDogClassify/test_DogClassify.py

https://github.com/zcemycl/algoTest/blob/main/py/solns/dogClassify/dogClassify.py

 

완전 탐색

선택 탐색

 

탐색 범위가 0 ~ 100 -> 37 ~ 68로 약 1/3 정도로 줄었으니 시간도 약 3배 줄어든 것을 확인했다.