[모두를 위한 딥러닝/시즌2] Lab-06 Softmax Classification

Lab-06 Softmax Classification

다음은 모두를 위한 딥러닝 시즌 2의 Lab-06 Softmax Classification를 학습하고 요약정리한 내용입니다. 강의 내용을 기반으로 요약하되, 보충 설명이 필요한 경우 부스트코스와 위키독스를 참고했습니다.

학습 목표

소프트맥스 분류(Softmax Classification)에 대해 알아본다.

핵심 키워드

소프트맥스(Softmax), 크로스 엔트로피(Cross Entropy)

 

library import 및 random seed 설정

이산 확률 분포

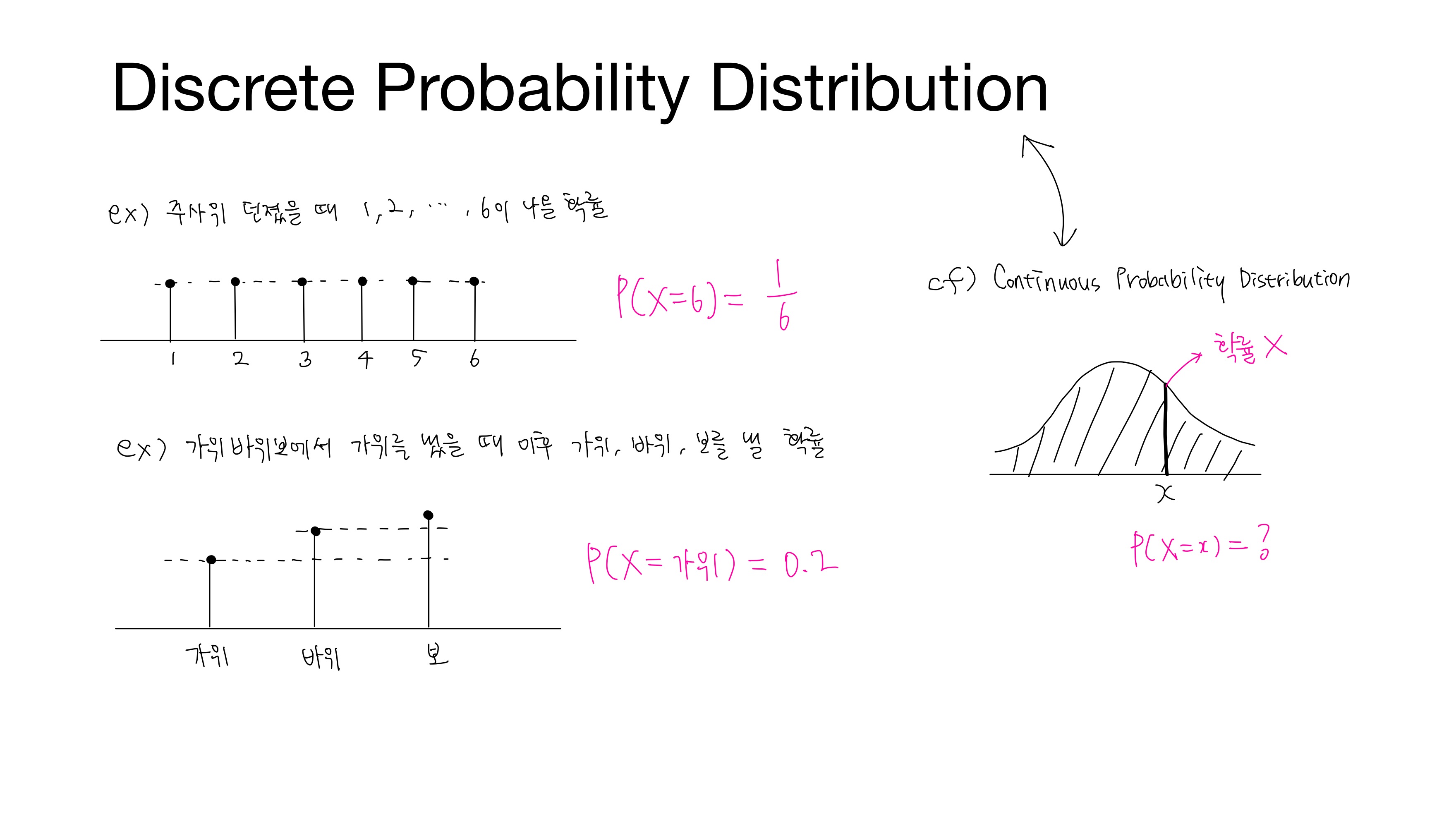
 • 이산 확률 분포(Discrete Probability Distribution)

확률 변수가 가질 수 있는 값들이 셀 수 있는 경우 그 확률 변수의 분포

 • 연속 확률 분포(Continuous Probability Distribution)

확률 변수가 가질 수 있는 값들이 셀 수 없는 경우, 즉 어떤 범위에 속하는 모든 실수인 경우 그 확률변수의 분포

위와 같은 이산 확률 분포에서 주사위를 던졌을 때 $6$이 나올 확률은 $\frac{1}{6}$로 확률이 존재하지만, 연속 확률 분포에서 한 점에서의 확률은 존재하지 않는다. 앞으로 다룰 소프트맥스는 이산 확률 분포를 따른다.

1. 소프트맥스(Softmax)

---

[1] i번째 클래스가 정답일 확률

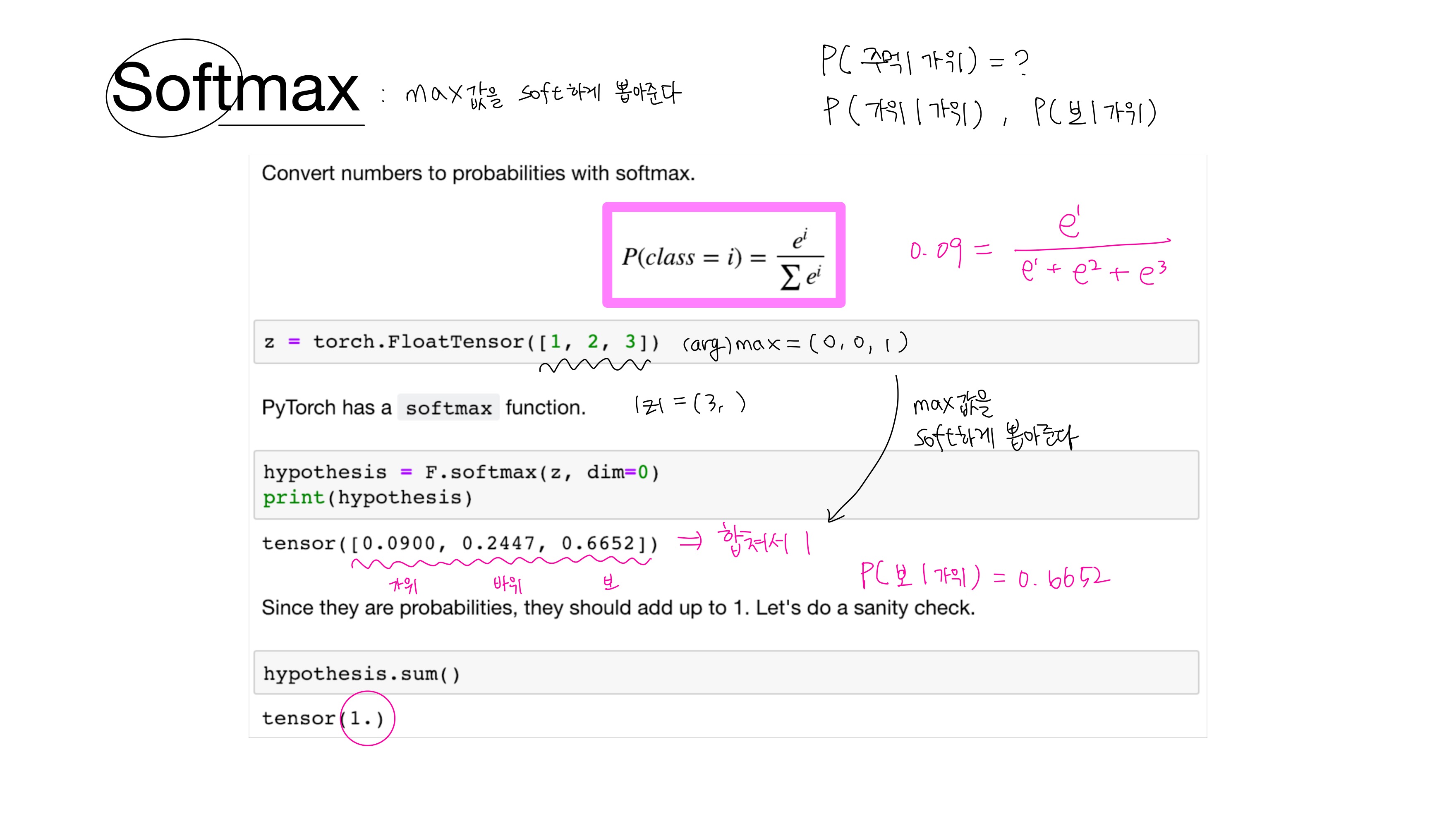
$z_i$ - $k$차원의 벡터에서 $i$번째 원소

 • 소프트맥스(Softmax) 함수

확률의 총합이 1이 되도록 각 클래스에 확률을 할당하는 함수로, 분류해야 하는 정답지(클래스)의 총 개수를 $k$라고 할 때 $k$차원의 벡터를 입력받아 각 클래스에 대한 확률을 추정한다.

[2] 클래스의 수가 총 k=3개인 경우

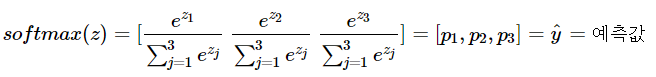
$p_1, p_2, p_3$는 각각 1, 2, 3번 클래스가 정답일 확률이고

0~1 사이의 값을 가지며 총합은 1이다.

2. 크로스 엔트로피(Cross Entropy)

---

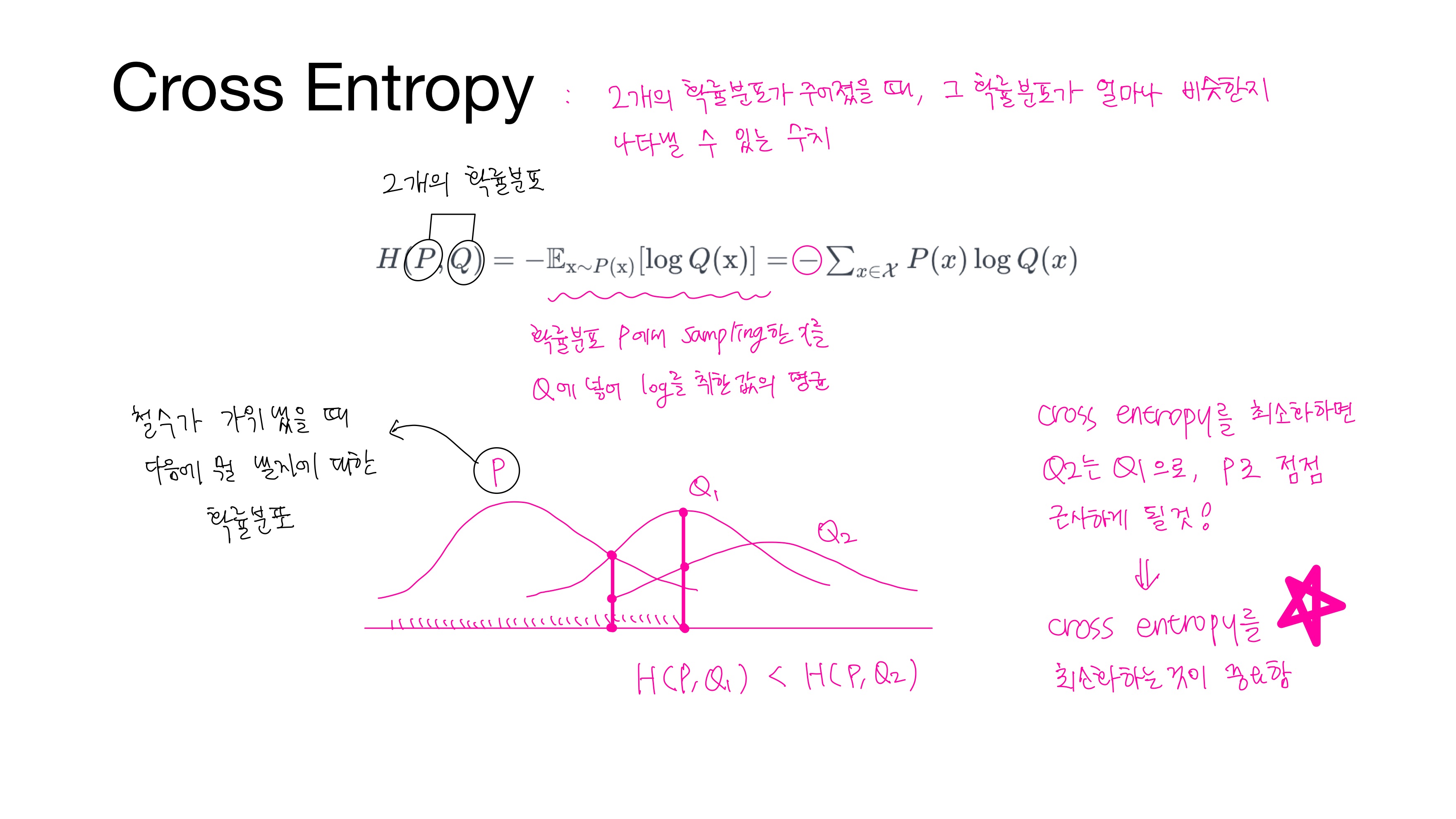
 • 크로스 엔트로피(Cross Entropy)

$P(x)$와 $Q(x)$라는 $2$개의 확률분포가 주어졌을 때, 그 확률분포가 얼마나 비슷한지 나타낼 수 있는 수치로,

크로스 엔트로피를 최소화하면 Q가 P에 가까워져 오차가 줄어들게 된다.

 

[3] 확률분포 P에서 sampling한 x를 Q에 넣어 log를 취한 것의 평균에 음수를 취한 것

 

위의 수식 [3]은 아래 수식 [4]로도 표현할 수 있다.

 

[4] 1개의 데이터에 대한 비용 함수

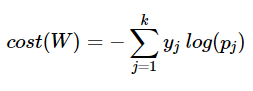
$y$는 실제값, $k$는 클래스의 개수

$y_j$는 실제값 원-핫 벡터의 $j$번째 인덱스

$p_j$는 샘플 데이터가 $j$번째 클래스일 확률이고, $\hat{y_j}$라고도 함

 

위의 수식 [4]를 n개의 전체 데이터에 대한 평균을 구하면 최종 비용 함수는 다음과 같다.

 

[5] n개의 전체 데이터에 대한 평균을 구한 비용 함수

 

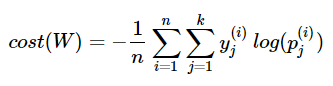
 • 원-핫 인코딩(One-hot encoding)

선택해야 하는 선택지의 개수만큼의 차원을 가지면서,

각 선택지의 인덱스에 해당하는 원소에는 1, 나머지 원소는 0의 값을 가지도록 하는 표현 방법

 • 원-핫 벡터(one-hot vector)

원-핫 인코딩으로 표현된 벡터

각 클래스가 순서의 의미를 갖고 있다면 회귀를 통해서 분류 문제를 풀 수도 있으나, 대부분의 다중 클래스 분류 문제가 각 클래스 간의 관계가 균등하다는 점에서 원-핫 벡터가 적절한 표현 방법이다.

 • F.log_softmax()

= F.softmax() + torch.log()

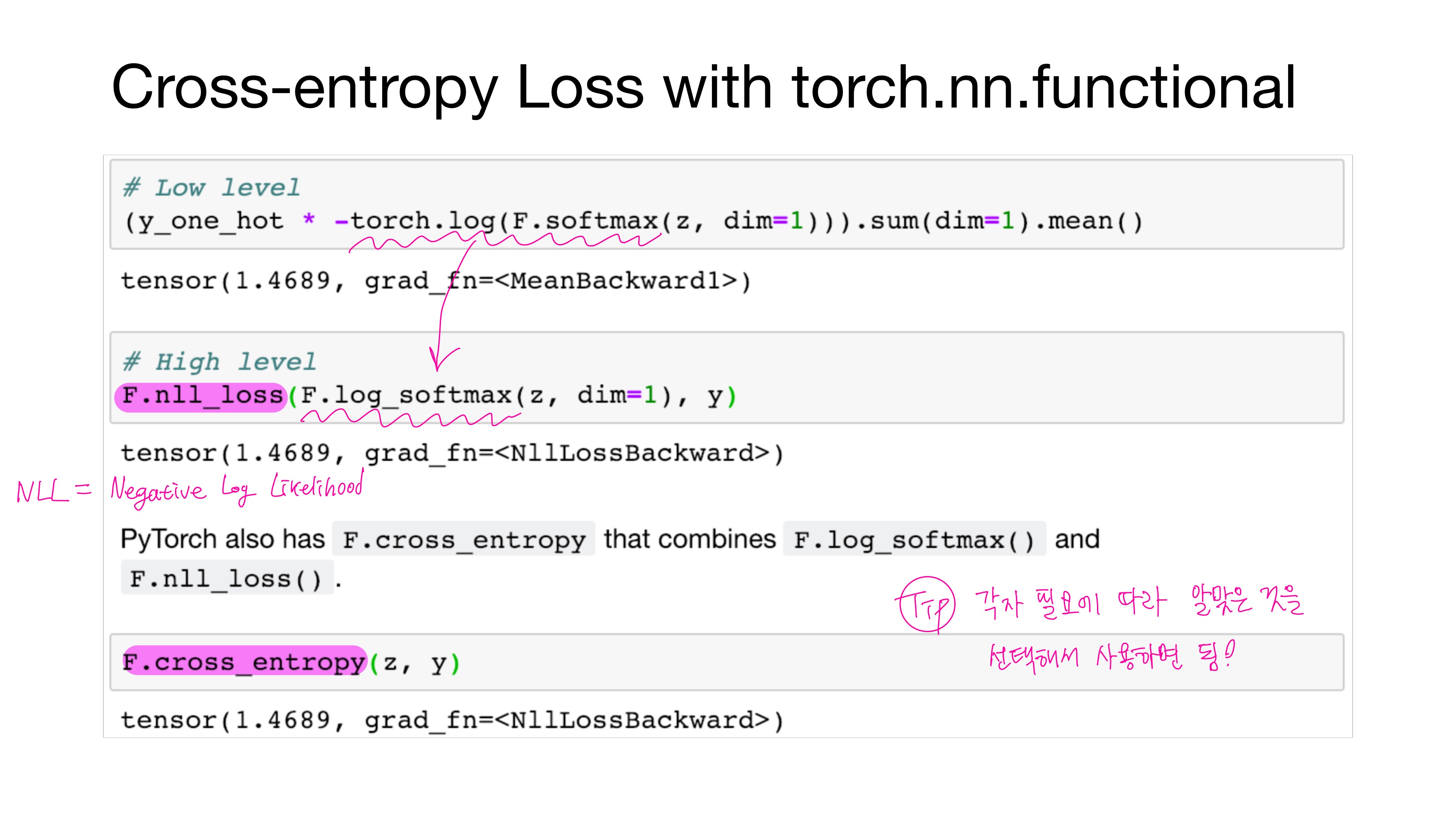
 • F.nll_loss()

nll이란 negative log likelihood로, F.log_softmax()를 수행한 후 남은 수식들을 수행한다.

 • F.cross_entropy()

= F.log_softmax() + F.nll_loss()

F.cross_entropy는 비용 함수에 소프트맥스 함수까지 포함하고 있음을 기억하고 있어야 구현 시 혼동하지 않는다.

3. 낮은 수준의 구현(Low-level Implementation)

---

앞서 말했듯이 F.cross_entropy()는 그 자체로 소프트맥스 함수를 포함하고 있으므로 Cost 계산 (1)과 달리 Cost 계산 (2)에서는 가설에서 소프트맥스 함수를 사용할 필요가 없다.

4. 높은 수준의 구현(High-level Implementation)

---

실전에서는 모델을 class로 구현

 • 이진 분류(Binary Classification)

로지스틱 회귀를 통해 2개의 선택지 중에서 1개를 고르는 문제

Cost는 Binary Cross Entropy
Hypothesis는 sigmoid

 • 다중 클래스 분류(Multi-Class Classification)

소프트맥스 회귀를 통해 3개 이상의 선택지 중에서 1개를 고르는 문제

Cost는 Cross Entropy
Hypothesis는 softmax