풀이 과정

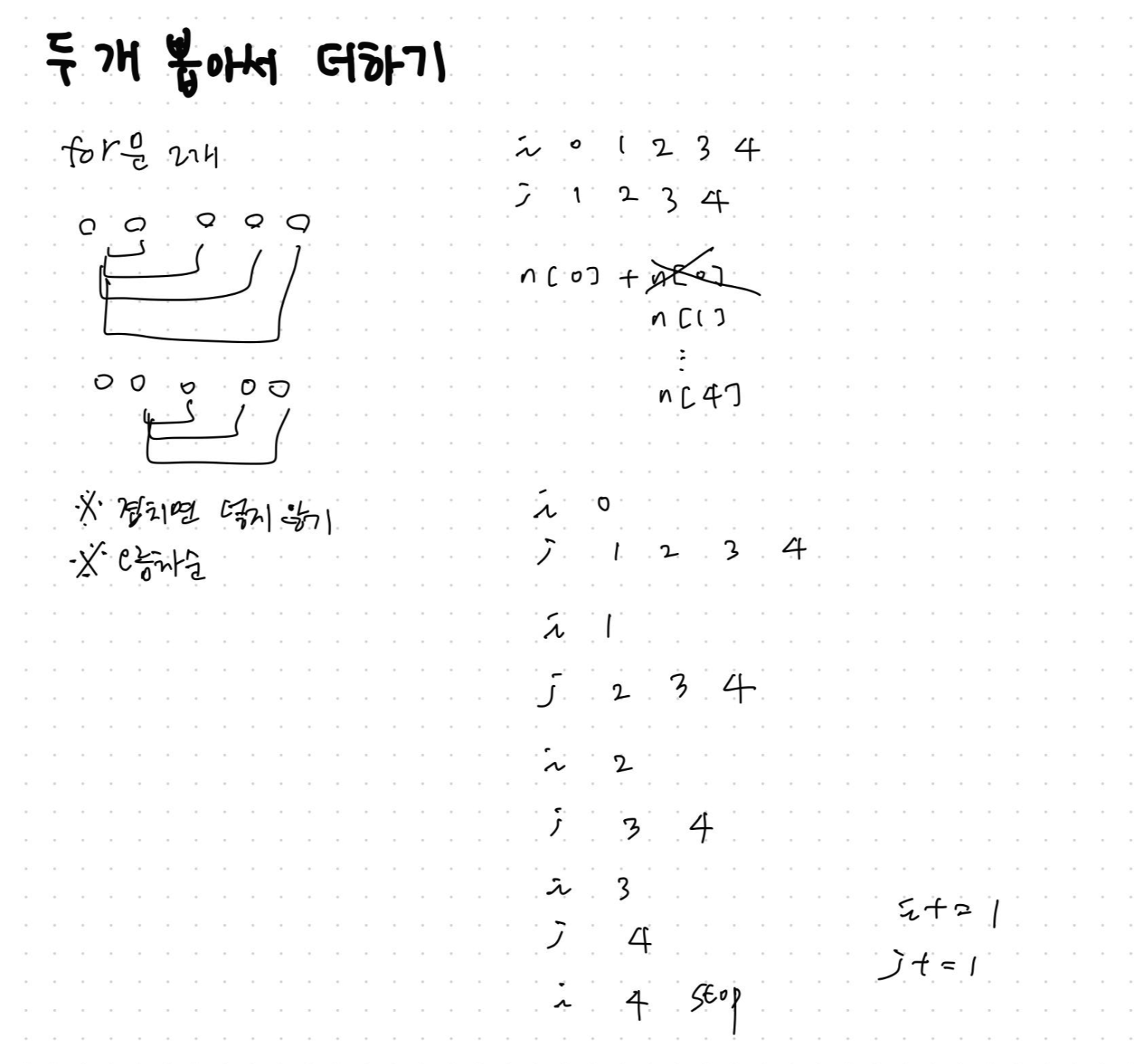
이번 문제는 저번 문제(크레인 인형뽑기 게임)보다 설명이 간단했고, 난이도도 쉬웠다. '서로 다른 인덱스에 있는 두 개의 수를 뽑아 더해서 만들 수 있는 모든 수'를 보고 for문을 두번 돌아야겠다는 생각이 들어 메모했다.
그리고 예시를 보고 중복되지 않는다는 점을 발견했다. 'for문 2개'만으로는 구체적이지 않아 예를 들어 어떤 식으로 두 개의 수를 더해야 하는지 메모에 그림을 그려놨고 주의해야 할 사항(겹치면 넣지 않기, 오름차순)을 따로 메모했다. 주의해야 할 사항은 나중에 까먹을 수 있으니 ※기호로 항상 메모해야 한다!
def solution(numbers):
answer = []
for i in range(len(numbers)):
for j in range(len(numbers)):
new_number = numbers[i] + numbers[j]
if new_number not in answer:
answer.append(new_number)
print(sorted(answer))
return sorted(answer)
for문 두개를 먼저 만들었다. 그리고 두 개의 수를 뽑아 더해서 만든 수를 new_number라는 변수에 담고 만약 answer라는 배열에 없다면 넣도록 해 중복을 방지했다. 그리고 마지막에 sort()를 쓸까 sorted()를 쓸까 고민하다가 sort()를 쓰게 되면 실제 배열이 정렬되지만(answer가 바뀜) 반환값이 없으므로 answer.sort() 후 return answer로 총 두줄이 된다. 하지만 sorted()를 쓰면 실제 배열이 정렬되진 않지만(answer는 바뀌지 않음) 바로 정렬된 배열을 반환해주기 때문에 return sorted(answer) 한 줄로 구현했다.
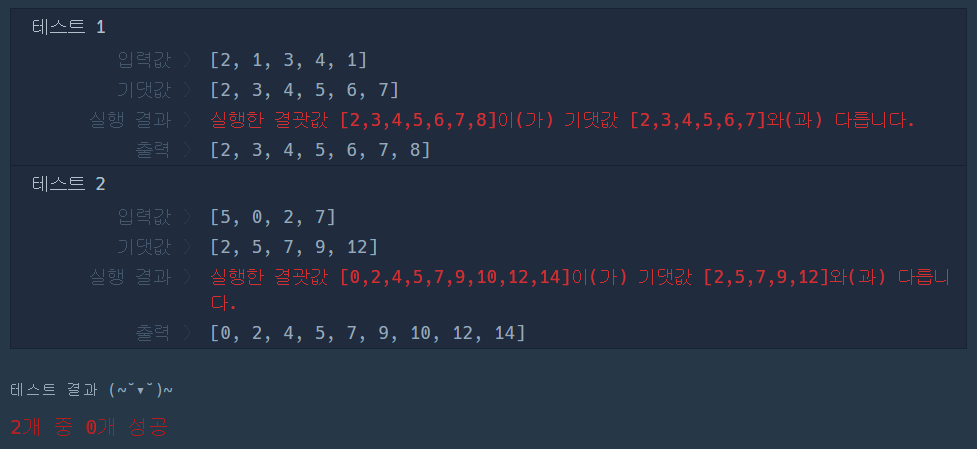
출력해보니 예제와 결과가 달랐다. '왜지?'싶어서 보니 같은 인덱스에 있는 두 개의 수도 더하고 있었다! 여기서부터 조금 어려웠다. 진짜 쉬운 문제인데 생각보다 구현이 바로 안됐다. 같은 인덱스끼리는 더하지 않으면서 또 자신보다 이전의 인덱스와는 더할 필요가 없었다(여기서 조합을 생각했어야 했다T^T) for j in range(1, len(numbers))을 했다가 for j in range(i+j, len(numbers))을 했다가 점점 꼬였다...

그러다 문득 지난 실수들이 생각났다. 지난번에 분명 개념을 생각하고 이를 문제에 녹이기로 하지 않았는가! 문제를 다시 읽어보고 순열과 조합이 생각났고 itertools 라이브러리가 떠올랐다! 여기에 라이브러리를 써도 되나 긴가민가하면서 파이썬 순열 조합을 구글링했다.
python 순열, 조합 구현
여러 기업들의 코딩 테스트를 준비하다보면 완전 탐색을 해야하는 문제가 많은데, 그런 문제를 만났을때 가장 직관적이기도 하고 쉽게 생각나는 것이 주어진 조건에 맞는 순열 혹은 조합을 모
medium.com
from itertools import permutations
def solution(numbers):
answer = []
for i, j in list(permutations(numbers,2)):
new_number = i + j
if new_number not in answer:
answer.append(new_number)
return sorted(answer)
위의 링크를 참고하여 다시 작성해보았다. 5번째 줄의 list(permutations(numbers, 2))는 numbers 배열에서 중복을 허용하지 않고 2개를 뽑아서 나열한다. numbers가 [5, 0, 2, 7]이라면 list(permutations(numbers, 2))는 [(5, 0), (5, 2), (5, 7), (0, 5), (0, 2), (0, 7), (2, 5), (2, 0), (2, 7), (7, 5), (7, 0), (7, 2)]이다.

결과는 성공! 이거 보고 바로 노트북 껐던 것 같다. 오늘 "알고리즘 공부 끝~" 이러면서^^ 하지만 지금부터가 시작이다.
다른 사람의 풀이
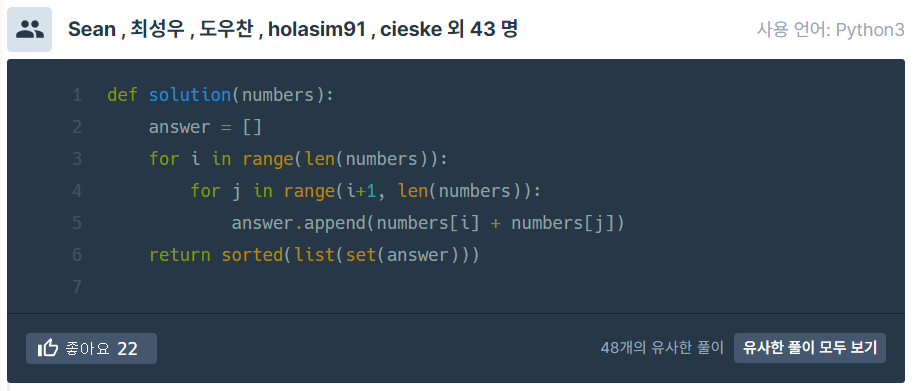
일단 itertools를 안 썼다는 것에 1차 놀랐고, 내가 itertools를 안 쓰고 코드를 쓴 것과 이 풀이에 상당히 근접했는데 i+1에 또 놀랐고, set을 써서 중복을 제거한 것에 3차 놀랐다. 그렇다. for new_number not in answer보다 set 쓰는 것이 훨씬 간결하다. 라이브러리를 사용하지 않고 좀 더 고민했다면 'i+1을 생각하지 않았을까?' 하는 아쉬움이 들었다.

itertools 라이브러리를 사용한 답안도 찾아봤는데 combinations보고 얼음... 그러고 보니까 내가 왜 순열을 썼지? 순서가 왜 중요하지? 으아아아아아악 나는 개념조차 제대로 안 되어 있었다... 문제 맞추기만 급급한 내 자신 반성해 제발
개념 정리
순열(permutation)
n개 중에 r개를 고른 것 (순서 O)
${}_n\mathrm{P}_{r} = \frac{n!}{(n-r)!}$
조합(combination)
n개 중에 r개를 고른 것 (순서 X)
${}_n\mathrm{C}_{r} = \frac{{}_n\mathrm{P}_{r}}{r!} = \binom{n}{r} = \frac{n!}{(n-r)!r!}$
순열과 조합은 둘 다 n개 중에 r개를 고른 것이나 순열은 순서를 고려하고, 조합은 순서를 고려하지 않는다. 개념 정의는 이상화 교수님의 <기초 확률 및 통계>를 참고했다.
앞서 본 케이스를 예로 들어보면 numbers가 [5, 0, 2, 7]이라고 하자. 4개 중에 순서를 고려해 2개를 고른다면 (5, 0), (5, 2), (5, 7), (0, 5), (0, 2), (0, 7), (2, 5), (2, 0), (2, 7), (7, 5), (7, 0), (7, 2)으로 총 12가지의 경우의 수가 나온다. 여기서는 (5, 0)과 (0, 5)가 서로 다른 경우이다! 하지만 순서를 고려하지 않는다면 (5, 0)과 (0, 5)는 결국 같은 경우이기에 조합은 (5, 0), (5, 2), (5, 7), (0, 2), (0, 7), (2, 7)로 총 6가지이다.
가령 반 전체에서 반장과 부반장을 뽑는다면 반장과 부반장은 다르기 때문에 순서가 중요하다. 이 때는 순서를 고려한 순열을 써야 한다. 하지만 반 전체에서 청소당번 2명을 뽑는다면 순서가 중요하지 않으므로 조합을 써야 한다.
(Python) 순열, 조합, 중복순열, 중복조합 쉽게 구현하기
(Python) 순열, 조합, 중복순열, 중복조합 구현하기 (Python) 순열, 조합 쉽게 만들기¶ 결론부터 말하자면, 라이브러리에서 불러온 함수와 직접 구현한 함수가 속도차이 10배정도를 보였
juhee-maeng.tistory.com
그리고 itertools에서 어떻게 순열과 조합을 구현하는지는 이미 잘 써놓은 글이 있기 때문에 이를 참고하면 될 것 같다.
오늘 깨달은 점을 정리해보면서 마무리하려고 한다.
- 순열은 순서를 고려한 것, 조합은 순서를 고려하지 않은 것!
- 중복 제거 시 set 기억!
코드
GitHub - leeejihyun/algorithm: 알고리즘 문제 풀이
알고리즘 문제 풀이. Contribute to leeejihyun/algorithm development by creating an account on GitHub.
github.com
출처
프로그래머스 코딩 테스트 연습 https://programmers.co.kr/learn/challenges
'Computer Science > 알고리즘' 카테고리의 다른 글
| [이코테] 큰 수의 법칙 (0) | 2022.01.02 |
|---|---|
| [프로그래머스/레벨1] K번째수 (0) | 2021.07.13 |
| [프로그래머스/레벨1] 모의고사 (0) | 2021.01.09 |
| [프로그래머스/레벨1] 완주하지 못한 선수 (0) | 2021.01.07 |
| [프로그래머스/레벨1] 크레인 인형뽑기 게임 (0) | 2021.01.04 |



