혼동 행렬 (Confusion Matrix)
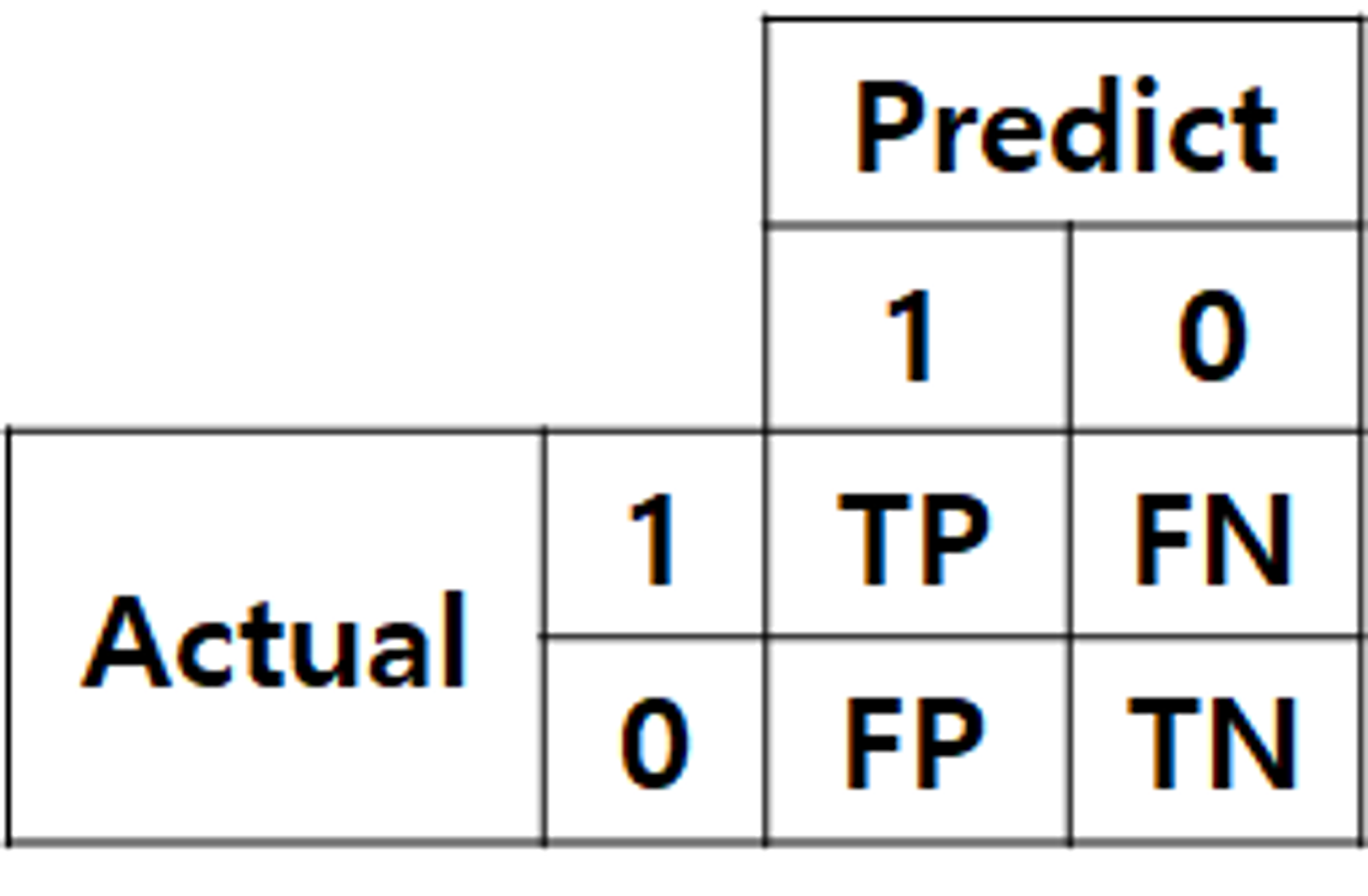
percision과 recall
- precision과 recall의 차이는 FP에 focus가 있는지, FN에 focus가 있는지
- FP가 가장 위험한 상황이라 이를 줄이고 싶다면 precision이 중요
- 반대로, FN이 가장 위험한 상황이라 이를 피해야 한다면 recall이 중요
- FP (False Positive): positive로 잘못 예측
- FN (False Negative): negative로 잘못 예측
precision (정확도, 정밀도)
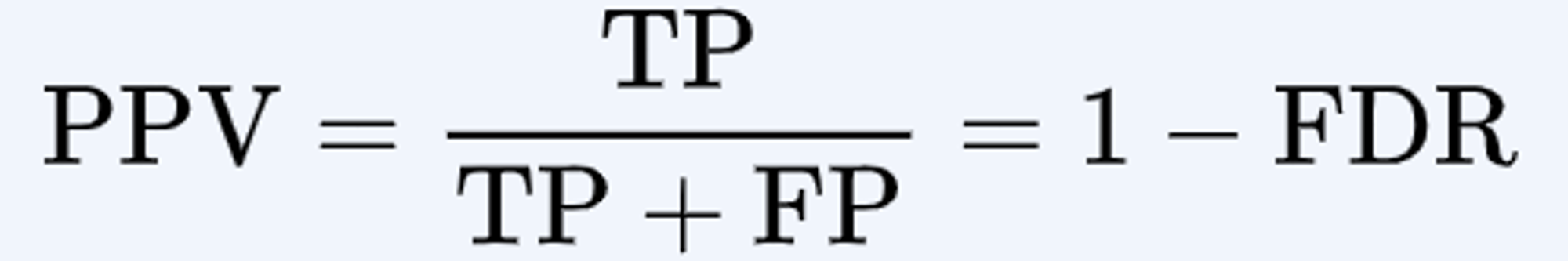
- 내가 맞다고 생각한 것 중에 얼마나 맞췄는지
- Positive Predictive Value
- 모델이 Positive로 예측한 샘플 중에서 실제로 Positive인 샘플의 비율을 나타냅니다. 즉, 모델이 얼마나 정확하게 Positive 클래스를 예측하는지를 측정
- ex) 지문인식
- 지문인식에서 가장 위험한, 치명적인 경우는 내가 아닌데 나로 인식해서 잠금이 해제되는 상황
- 나로 예측하는 경우 중에 정답이 많아야 하므로
- 그렇다 보니 내가 맞는데도 잠금 해제가 안 되는 경우가 많음
recall (검출률, 재현율)
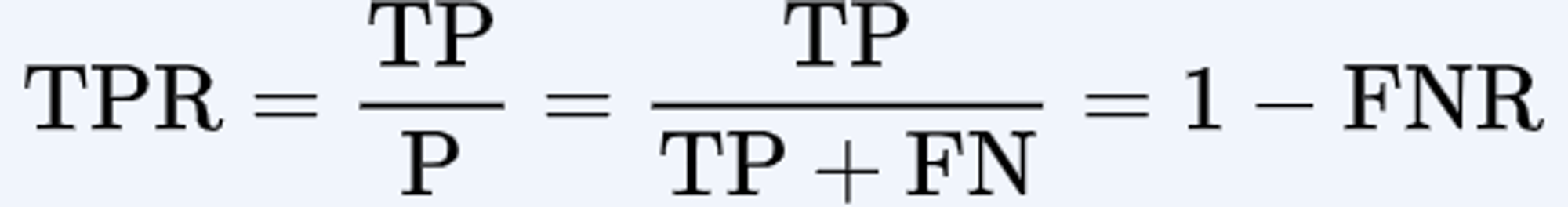
- 진짜 정답 중에 몇개나 맞췄는지
- Sensitivity,
Hit Rate, True Positive Rate - 실제로 Positive인 샘플 중에서 모델이 Positive로 예측한 샘플의 비율을 나타냅니다. 즉, 모델이 Positive 클래스를 얼마나 잘 감지하는지를 측정
- ex) 화재경보기
- 최악의 상황은 불이 안났는데 불이 났다고 예측하는 경우보다 불이 났는데 안났다고 예측하는 경우
- 진짜 화재 중에 예측한 화재가 더 많아야 하기 때문
- 그렇다 보니 담배연기만 피워도 화재경보기가 작동하는 경우가 많음
F1-Score
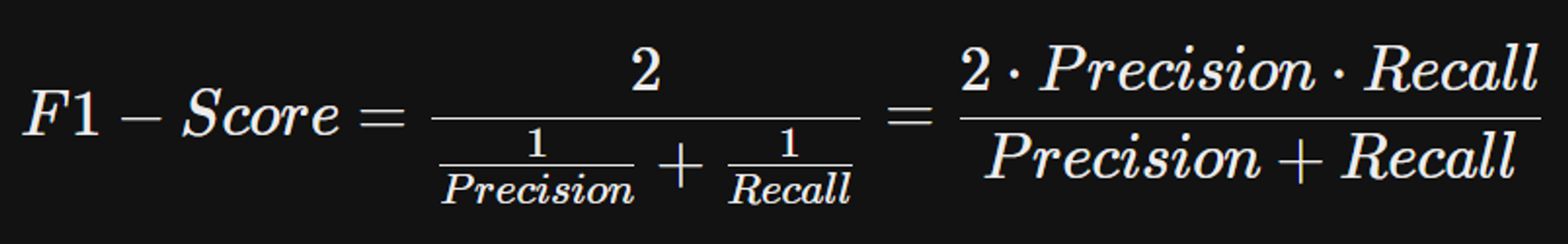
- 정밀도(Precision)와 재현율(Recall)의 조화 평균(Harmonic Mean)
- 조화평균 → 두 지표 간의 균형을 잘 반영
- 특히 불균형한 클래스 분포를 가진 데이터셋에서 유용
- 왜?
- 클래스 불균형 문제에서는 주로 샘플 수가 적은 클래스에 대한 Recall을 높이는 것이 중요합니다. 왜냐하면 샘플 수가 적은 클래스에 대한 Recall이 낮으면, 모델이 해당 클래스를 올바르게 감지하지 못할 수 있기 때문입니다. 예를 들어, 양성 클래스가 드물게 발생하는 의료 진단 문제에서, 거의 없는 양성 클래스에 대한 Recall이 낮으면 실제로 중요한 질병을 감지하지 못할 수 있습니다.
- 그러나 샘플 수가 적은 클래스에 대한 Recall을 높이려고 하면 다수 클래스에 대한 Precision이 낮아지게 됩니다. 클래스 불균형 문제에서는 주로 Recall을 높이는 것이 중요하지만, 이 과정에서 Precision을 유지하는 것도 중요합니다. 이는 샘플 수가 적은 클래스에 대한 Recall을 고려하면서도, 다수 클래스에 대한 Precision을 최대한 유지하여 모델이 잘못된 양성 예측을 최소화하기 위함입니다.
- 이 둘의 조화평균으로 지표를 만들면 precision, recall을 둘다 균형있게 반영하기 때문에두 지표가 균형을 이룰 때 가장 큰 값을 가집니다. 따라서, 특히 불균형 클래스 분포를 가진 데이터셋에서 유용합니다.
- 조화평균은 주어진 값들의 역수를 취하기 때문에 큰 값은 작게, 작은 값은 크게 만들어줘 전체적으로 균형을 이루는 특성
- 왜?
ROC 곡선과 AUC
ROC 곡선 (Receiver Operation Characteristic Curve)
- 수신자 판단 곡선 → 원래 2차대전 때 통신 장비 성능 평가를 위해 고안된 수치
- FPR(False Positive Rate,
재현율, 민감도)이 변할 때 TPR(True Positive Rate)이 어떻게 변하는지를 나타내는 곡선- FPR을 0부터 1까지 변경. ← 분류 결정 임곗값을 1부터 0까지 변경
AUC (Area Under Curve)
- 이진 분류의 예측 성능 측정에서 중요하게 사용되는 지표
- AUC가 커지려면 FPR이 작은 상태에서 얼마나 큰 TPR을 얻을 수 있느냐가 관건
L1 규제 (L1 Reguralization), L2 규제 (L2 Regularization)
- 일반적으로 L1 규제는 feature가 많고 그 중 일부만 중요한 경우에 유용하며, L2 규제는 모든 feature가 비슷한 영향력을 갖는 경우에 유용
L1 규제 (L1 Reguralization)
- 가중치의 절대값에 비례하는 항을 손실 함수에 추가하는 방식
- L1 규제는 가중치의 일부를 0으로 만들어 특성 선택을 자동으로 수행하는 경향이 있습니다. 즉, 일부 특성의 가중치를 완전히 제거하여 모델을 더 간단하게 만들 수 있습니다.
- L1 규제는 희소한 가중치 벡터를 생성할 수 있습니다. 즉, 대부분의 가중치가 0이거나 매우 작은 값을 갖는 경우가 많습니다.
L2 규제 (L2 Regularization)
- 가중치의 제곱에 비례하는 항을 손실 함수에 추가하는 방식
- L2 규제는 특성 선택을 자동으로 수행하지 않으며, 대신 모든 특성을 고려한 채로 가중치를 줄입니다.
- L2 규제는 가중치를 크게 줄여주는 경향이 있지만, 0으로 만들지는 않습니다. 모든 특성이 포함된 모델을 유지하면서 가중치의 크기를 줄이는 데 중점을 둡니다.
조기 중단 (Early Stopping)
validation/test loss가 더이상 낮아지지 않을 때 stop
출처: ChatGPT, <파이썬 머신러닝 완벽 가이드>
'용어정리' 카테고리의 다른 글
| 추천 관련 용어 정리 (0) | 2024.02.18 |
|---|---|
| 딥러닝 용어 정리 및 책 추천 (0) | 2020.12.30 |
| C++ 용어 정리 및 사이트 추천 (0) | 2020.12.26 |
